L’objet de cette partie est de présenter les méthodes d’acquisition d’informations géométriques sur des objets par levé direct sur le terrain. L’ensemble des méthodes présentées ont chacune des spécificités, des conditions d’application et d’exécution précises.
3.1. Eléments de base sur les appareils topographiques
Présents dans tous les appareils professionnels qui seront évoqués dans la suite de ce cours, les nivelles et les lunettes sont des pièces majeures. Par conséquent, il convient d’en préciser la constitution et le principe de fonctionnement. Le réglage et la vérification de ces éléments très sensibles ne sera pas abordé ici, et il est conseillé de faire appel à un professionnel pour effectuer ces opérations.
3.1.1. Un point sur le vocabulaire
Ces précisions sémantiques concernent autant les appareils que les méthodes topographiques. Elles se concrétiseront au fil de l’avancée du cours.
Axe de visée, axe de collimation : ligne passant par les foyers de l’objectifs d’une lunette et le point de mesure en correspondance avec le réticule.
Basculement : la lunette du théodolite est tournée de 200 gr autour de l’axe horizontal pour éliminer les erreurs instrumentales.
Calage et mise en station : opération effectuée par l’opérateur pour amener l’axe vertical de l’appareil à l’aplomb d’un repère sur le sol.
Correction : valeur algébrique à ajouter à une valeur observée ou calculée pour éliminer les erreurs systématiques connues.
Croisée du réticule : croix dessinée sur le réticule représentant un point de l’axe de visée.
Erreur de fermeture : écart entre la valeur d’une grandeur mesurée en topométrie et la valeur fixée ou théorique.
Fils stadimétriques : lignes horizontales marquées symétriquement sur la croisée du réticule. Elles sont utilisées pour déterminer les distances à partir d’une échelle graduée placée sur la station.
Hauteur de l’appareil : distance verticale entre l’axe horizontal de l’appareil et celle de la station.
Implantation : établissement de repères et de lignes définissant la position et le niveau des éléments de l’ouvrage à construire.
Levé : relevé de la position d’un point existant.
Lunette : instrument optique muni d’une croisée de réticule ou d’un réticule, utilisé pour établir un axe de visée par l’observation d’un objet de mesure.
Mesurage : opérations déterminant la valeur d’une grandeur.
Nivelle : tube en verre scellé, presque entièrement rempli d’un liquide (alcool) dont la surface intérieure a une forme bombée obtenue par moulage, de sorte que l’air enfermé forme une bulle qui prend différentes positions suivant l’inclinaison du tube.
Nivellement : opération consistant à mettre une ligne ou une surface dans la position horizontale, ou mesurage de différences de niveaux.
Repères : points dont on connaît les coordonnées.
Réticule : disque transparent portant des traits ou des échelles. Il permet d’effectuer correctement des lectures.
Signal, balise : dispositif auxiliaire pour indiquer l’emplacement d’une station (par un jalon).
Station : tout point à partir duquel ou vers lequel on effectue une mesure. Cela peut être un point spécifié sur un bâtiment ou un point marqué dans la zone d’étude.
Tolérance : variation admissible pour une dimension.
La nivelle se décline essentiellement en deux types : la section de tore et la section de sphère. Le but de cet instrument est de contrôler le calage d’un point, d’un plan, d’un axe de visée… On parle généralement de sensibilité de la nivelle pour qualifier la "vitesse" à laquelle va réagir la bulle. La valeur indiquée dans les documentations constructeur se réfère généralement à l’angle d’inclinaison nécessaire au déplacement de la bulle de une division (couramment 2mm). De façon générale, les nivelles toriques sont beaucoup plus sensibles, et précises que les nivelles sphériques. Ces dernières sont d’ailleurs généralement utilisées pour effectuer des calages rapides, avant l’emploi de nivelles électroniques et/ou la mise en action de dispositifs de compensation (cf. §3.2.1.1).
Les lunettes sont des systèmes optiques comprenant un réticule et plusieurs lentilles, dont un dispositif de mise au point. Le système optique est caractérisé par les grandeurs classiques de l’optique géométrique : champ, grossissement…
Le réticule est le dispositif de lecture et de visée. Ce jeu de lignes (Figure 1) est actuellement gravé sur une lame à faces parallèles, mais en d’autres temps, on utilisait des toiles d’araignée d’Afrique !!

Figure 1. Exemple de réticule, avec fils stadimétriques
NB : la différence des lectures sur mire sur chacun des fils stadimétriques est une évaluation de la distance entre l’appareil et la mire, à une constante près. Cette constante, dite stadimétrique, est souvent de 100, et est précisée dans la documentation des appareils.
3.2. Détermination des altitudes
Les méthodes de détermination des altitudes ont connu un grand essor pendant les grandes périodes d’urbanisation et de viabilisation des espaces habités. L’objectif de ces mesures est de connaître précisément l’altitude de points, généralement pour assurer les écoulements. Par conséquent, la surface de référence la plus souvent considérée est le géoïde, par la connaissance de la verticale du lieu.
Les techniques de détermination des altitudes qui sont présentées ici diffèrent entre elles d’une part par le type d’instrument utilisé et la méthodologie, mais aussi par la précision que l’on peut en attendre. Bien évidemment, plus la précision recherchée est grande, plus les protocoles sont lourds à mettre en œuvre et les instruments coûteux à acquérir.
3.2.1.1. Nivellement direct ou géométrique
Les méthodes de nivellement direct constituent l’arsenal le plus efficace pour déterminer l’altitude de points particuliers. La précision des déterminations dépend du matériel employé (cf. §3.2.2) mais aussi et surtout, des méthodes, ce que nous allons aborder maintenant :
· Nivellement par rayonnement : la première mesure est effectuée sur un point d’altitude connue, de façon à déterminer l’altitude du plan de visée. A partir de là, toutes les altitudes sont déterminées par différence par rapport à ce plan. Cette méthode permet de lever rapidement un semis de points matérialisés (sondages, points de berges, de fonds…). Elle présente néanmoins l’inconvénient de n’offrir aucun contrôle sur les déterminations : toute erreur de lecture est indétectable et fatale.
·
 Nivellement
d’itinéraires par cheminement : c’est la méthode la plus couramment
employée pour déterminer les altitudes de points matérialisés, non situés à une
même distance d’une seule station d’appareil. Elle est également plus sûre,
quant aux éventuelles erreurs de lecture, et plus intéressante du point de vue
de la précision des déterminations : on dispose de méthodes de
compensation des erreurs très efficaces. Plusieurs règles sont appliquées pour
minimiser l’influence des erreurs systématiques et accidentelles : les
portées équidistantes, les contrôles de marche, le contrôle sur fermeture…
Nivellement
d’itinéraires par cheminement : c’est la méthode la plus couramment
employée pour déterminer les altitudes de points matérialisés, non situés à une
même distance d’une seule station d’appareil. Elle est également plus sûre,
quant aux éventuelles erreurs de lecture, et plus intéressante du point de vue
de la précision des déterminations : on dispose de méthodes de
compensation des erreurs très efficaces. Plusieurs règles sont appliquées pour
minimiser l’influence des erreurs systématiques et accidentelles : les
portées équidistantes, les contrôles de marche, le contrôle sur fermeture…
· Nivellement de franchissement : cette méthode est beaucoup plus difficile à mettre en œuvre et s’applique dans le cas de franchissement de vallées, où le principe des portées équidistantes est inapplicable. On travaille dans ce cas simultanément avec deux appareils, de part et d’autre de l’obstacle (le cas idéal étant de pouvoir les aligner avec les mires), afin de minimiser les erreurs instrumentales et atmosphériques.
· Nivellement d’auscultation : cette dernière méthode a pour objectif de déterminer la cote d’un repère et ses variations dans le temps (barrage, pont, bâtiment). Elle nécessite l’application de tous les principes énoncés précédemment, et plus encore : équidistance, réglage optimal du niveau, mires en invar, contrôles, problèmes de réfraction accidentelle (intérieur/extérieur d’un bâtiment), sûreté des repères…
Pour résumer :
 Le
principe du nivellement géométrique est la mesure d’une différence d’altitude,
ou d’une succession de différences, par rapport à un plan ou un point connu. Il
est réalisé au niveau, et la précision des mesures peut aller de 1/10ème
de mm à quelques mm, selon les matériels et protocoles mis en œuvre.
Le
principe du nivellement géométrique est la mesure d’une différence d’altitude,
ou d’une succession de différences, par rapport à un plan ou un point connu. Il
est réalisé au niveau, et la précision des mesures peut aller de 1/10ème
de mm à quelques mm, selon les matériels et protocoles mis en œuvre.
De manière générale, la relation entre l’altitude du point de départ R1 et le point d’arrivée R2 d’un nivellement par cheminement est donné par la relation :
![]() Eq.
1
Eq.
1
où AR représente les lectures Arrière (en rapport à la direction de l’itinéraire), et AV les lectures Avant.
Lorsque les altitudes des points de départ et d’arrivée sont connus, on peut alors calculer la fermeture du cheminement :
![]() Eq.
2
Eq.
2
Cette erreur de fermeture, normalement due aux erreurs accidentelles, doit être répartie sur l’ensemble du cheminement et de ses mesures. Les différentes méthodes disponibles seront abordées au paragraphe 3.4.2.
3.2.1.2. Nivellement indirect ou trigonométrique
A la différence, le nivellement trigonométrique est réalisé par calcul de la dénivelée à partir de la distance oblique entre les points, et l’angle (également appelé distance) zénithal. Le principe général est explicité par la figure ci-dessous.

Figure 2. Principe du nivellement trigonométrique
Selon ce schéma, l’altitude du point B peut être reliée à celle du point A par la relation :
![]() Eq.
3
Eq.
3
Nous avons précédemment affirmé que la méthode du nivellement direct ou géométrique était beaucoup plus précise que celle-ci. Cela vient essentiellement du mode de détermination des différentes variables : hi est mesuré au ruban (au centimètre, voire au demi centimètre près) comme la hauteur de prisme HP, puis, interviennent les précisions de mesure sur la distance oblique et l’angle vertical. Il est néanmoins très utile pour déterminer la hauteur de point inaccessible (cf. fiches techniques).
Le nivellement trigonométrique peut être employé selon la méthodologie du cheminement. Ainsi, il n’est pas nécessaire de déterminer ni la hauteur d’appareil hi, ni la hauteur de prisme (qui doit cependant rester constante pour une même station). On n’exploite alors que la distance oblique et la distance zénithale.
Les autres techniques de nivellement pourront peut-être paraître marginales, mais elles méritent cependant d’être citées. La première est le nivellement barométrique, qui exploite la chute de pression atmosphérique avec l’augmentation de l’altitude. Ce principe est utilisé dans la majorité des altimètres de sport, appareils qui doivent être recalés régulièrement pour leur assurer une efficacité maximale. Une seconde est constitué par les méthodes de nivellement hydrostatique. Il permet, par le principe des vases communicants, de réaliser un nivellement de haute précision, en permanence opérationnel sur un ouvrage.
3.2.2. ![]() Les
appareils
Les
appareils
 Le
niveau est l’appareil employé pour le nivellement direct. L’indirect quant à
lui, utilise le théodolite, que nous détaillerons dans la partie suivante (cf.
§3.3.3).
Le
niveau est l’appareil employé pour le nivellement direct. L’indirect quant à
lui, utilise le théodolite, que nous détaillerons dans la partie suivante (cf.
§3.3.3).
· Le niveau de chantier : constitue le matériel le plus simple et le moins onéreux. Il offre généralement une précision très moyenne et est d’une mise en œuvre simple. Le calage est assuré par une nivelle torique.
· Le niveau automatique : constitue actuellement l’entrée de gamme de la plupart des constructeurs (les niveaux de chantiers sont de plus en plus souvent automatiques). Il est doté d’un système qui permet de compenser le défaut de calage de l’appareil à la mise en station (prisme suspendu, réticule suspendu, systèmes pendulaires…). Le dispositif de calage est alors une nivelle sphérique.
· Le niveau numérique : se répand toujours plus chez les professionnels. D’une grande simplicité d’utilisation, il utilise des principes de compensation similaires au niveau automatique, une caméra CCD et une mire à code barres. Il permet alors de s’abstenir complètement de la mesure, et des erreurs qu’elle comporte.


|
1 |
|
|
2 |
|
|
|
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
3.2.3. Les réseaux de référence
Il existe plusieurs définitions de l’altitude, d’où plusieurs systèmes d’altimétrie. Le système en vigueur en France est appelé IGN69. Il est matérialisé sur le territoire par un maillage de points de différents ordres, exprimés en altitude normale. Cependant, à Strasbourg par exemple, trois systèmes coexistent :
· le système IGN 69, normal,
· le NGF (Nivellement Général de la France), orthométrique,
· et le NN (Normal Null) allemand, orthométrique.
Figure 3. L’altitude orthométrique
 Nous
avons vu plus haut qu’il existait plusieurs surfaces de référence. Pour
l’altimétrie, la surface physique de référence est le géoïde, normale en tout
point à la verticale du lieu. Il est cependant possible de réaliser différentes
mesures de hauteur au-dessus du géoïde. Lorsque cette mesure est effectuée
selon cette verticale, on parle alors de hauteur orthométrique. Par contre,
lorsque des mesures de gravimétrie sont réalisées, on accède à la valeur
moyenne de la pesanteur normale, définissant ainsi la hauteur normale. L’IGN
préconise pour ceci des mesures gravimétriques tout les kilomètres en terrain
accidenté, et tout les 10 km en terrain plat.
Nous
avons vu plus haut qu’il existait plusieurs surfaces de référence. Pour
l’altimétrie, la surface physique de référence est le géoïde, normale en tout
point à la verticale du lieu. Il est cependant possible de réaliser différentes
mesures de hauteur au-dessus du géoïde. Lorsque cette mesure est effectuée
selon cette verticale, on parle alors de hauteur orthométrique. Par contre,
lorsque des mesures de gravimétrie sont réalisées, on accède à la valeur
moyenne de la pesanteur normale, définissant ainsi la hauteur normale. L’IGN
préconise pour ceci des mesures gravimétriques tout les kilomètres en terrain
accidenté, et tout les 10 km en terrain plat.
 Les
repères de nivellement des réseaux de troisième et quatrième ordre sont
généralement des troncs de cône, scellés dans un mur de maison, d’église, de
cimetière… Il faut cependant être vigilant lors de l’utilisation de ce type de
matérialisation. En effet, l’expérience montre que lorsque des maisons sont
rénovées, ravalées, les repères sont enlevés puis replacés. Bien évidemment, la
valeur indiquée par la fiche signalétique correspondante est alors obsolète.
Méfiance !!
Les
repères de nivellement des réseaux de troisième et quatrième ordre sont
généralement des troncs de cône, scellés dans un mur de maison, d’église, de
cimetière… Il faut cependant être vigilant lors de l’utilisation de ce type de
matérialisation. En effet, l’expérience montre que lorsque des maisons sont
rénovées, ravalées, les repères sont enlevés puis replacés. Bien évidemment, la
valeur indiquée par la fiche signalétique correspondante est alors obsolète.
Méfiance !!
Il est actuellement possible d’obtenir la fiche signalétique des repères de nivellement, mesurés dans le système IGN 69, gratuitement auprès de l’IGN, via son site Internet (http://www.ign.fr ; ftp://ign.fr). Ce point est abordé en fin du chapitre suivant.
TD : calcul d’un
cheminement altimétrique
3.3. Détermination des coordonnées
Nous sommes à présent capables de déterminer, plus ou moins précisément, l’altitude de points particuliers du terrain. Il s’agit maintenant de les localiser en planimétrie.
3.3.1. Calcul d’orientation et de distances
Nous abordons ici quelques rappels sur le calcul d’angles et de distances à partir des coordonnées de points.
Le calcul de la distance, horizontale ou non, entre deux points de coordonnées connues est extrêmement simple puisqu’il résulte de l’application stricte du théorème de Pythagore. On rappelle ici la formule générale de calcul de la distance à partir des coordonnées tridimensionnelles des points A et B :
![]() Eq.
4
Eq.
4
Cette distance oblique peut être "rabattue" à la verticale, comme nous l’avons vu au paragraphe 3.2.1.2, et mesurer une dénivelée partielle. De la même façon, la distance horizontale peut être obtenue (Figure 2) :
![]() Eq.
5
Eq.
5
On définit le gisement comme l’angle, dans le plan horizontal, entre un vecteur, défini par deux points connus en coordonnées, et la direction du nord cartographique. Il est compté dans le sens horaire.
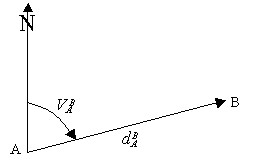
![]()
Figure 4. Définition du gisement
3.3.1.3. La transmission de gisement

Figure 5. Cheminement polygonal
On suppose que le gisement du premier segment, entre les deux premiers points Cn-2 et Cn-1 du cheminement est connu. Ainsi, le gisement du segment suivant est donné par la relation :
![]() Eq.
6
Eq.
6
Par conséquent, tout cheminement angulaire est calculé de proche en proche à partir des lectures L sur le cercle horizontal, et toujours à 200 grades près.
De façon générale, avant de lever les points de détails, il est nécessaire d’établir un canevas. Le principe est similaire à celui employé pour le nivellement par cheminement d’itinéraires : on détermine les coordonnées des points d’appui du canevas de proche en proche, à partir d’un point du réseau de référence.
3.3.2.1. Orientation de cheminements
Comme nous le verrons dans le paragraphe suivant, un théodolite est muni d’un dispositif de mesure des angles horizontaux. Afin de pouvoir déterminer les coordonnées de points à partir de points connus, il est nécessaire de déterminer l’orientation du zéro du cercle horizontal. Ce calcul est appelé la détermination du V0 de la station.


Figure 6. Orientation de canevas
Le cas le plus simple se trouve lorsque le premier point C1 est connu en coordonnées. On peut ainsi calculer les gisements des segments C1-Ai facilement, et les rattacher au gisement de la visée à 0 gon sur le cercle horizontal. Pour chaque visée sur un point d’appui, on peut déterminer un V0i, et leur moyenne donnera la V0 de la station.
![]() Eq.
7
Eq.
7
 Eq. 8
Eq. 8
On peut également pondérer les observations en fonction des distances, en utilisant la racine carrée de la distance comme facteur de poids. On prend ainsi mieux en compte les erreurs de pointés sur les cibles.
 Eq.
9
Eq.
9
 Cependant,
avec ou sans pondération des visées, la règle veut que les visées sur
références soient toujours beaucoup plus longues que celles sur les points de
canevas. C’est une condition nécessaire pour réduire l’influence des erreurs de
pointé sur les visées d’orientation.
Cependant,
avec ou sans pondération des visées, la règle veut que les visées sur
références soient toujours beaucoup plus longues que celles sur les points de
canevas. C’est une condition nécessaire pour réduire l’influence des erreurs de
pointé sur les visées d’orientation.
3.3.2.2. Observation du canevas
Plusieurs méthodes d’observation de canevas sont disponibles, souvent regroupées sous la dénomination de polygonale :
· La triangulation : qui consiste à observer les angles entre les différents segments du réseau.
· La trilatération : qui consiste à en observer les distances.
· La triangulatération, ou poylgonation : qui consiste à observer angles et distances entre les points du canevas. C’est la méthode la plus couramment employée pour les travaux usuels. Elle est d’ailleurs grandement facilitée par les appareils disponibles sur le marché.
Comme pour la détermination des altitudes, si les points de départ et d’arrivée sont connus, il est possible de déterminer les fermetures de la polygonale. La première est la fermeture angulaire, obtenue par la relation suivante :
![]() Eq.
10
Eq.
10
Le premier terme représente la somme théorique d’une polygonale à n cotés, et le second, la somme effective.
De même, il est utile de connaître les fermetures planimétriques en X et en Y, tout autant que la fermeture altimétrique. L’ensemble peut être regroupé dans la fermeture linéaire absolue :
![]() Eq.
11
Eq.
11
![]() Eq.
12
Eq.
12
où Xf représente la coordonnée X calculée du point final, et Xc sa valeur connue.
3.3.2.3. Les points de détails
La théorie voudrait que l’on commence par déterminer les points de canevas puis, lorsque leurs coordonnées sont calculées et vérifiées, on passe seulement au levé des points de détail. Pratiquement, le détail est levé en même temps que la polygonale pour des questions évidentes de rentabilité, même si ces précautions sont parfois prises sur des réalisations de grande envergure.
 Nous
partirons du principe que la station est correctement orientée : il est
recommandé, en début de station de procéder à toutes les observations sur
référence avant de commencer le levé de détails. Puis en fin de levé, il
est souhaitable de réaliser un contrôle des fermetures angulaires.
Nous
partirons du principe que la station est correctement orientée : il est
recommandé, en début de station de procéder à toutes les observations sur
référence avant de commencer le levé de détails. Puis en fin de levé, il
est souhaitable de réaliser un contrôle des fermetures angulaires.
Depuis une station orientée, les coordonnées de tout point de détail mesuré peuvent être obtenus par le triplet de formules suivant :
![]()
![]()
![]()
L’appareil de base pour les mesures d’angles. Il est essentiellement constitué, en plus de la lunette de visée, de deux cercles : un horizontal et un vertical. Nous allons ici en étudier brièvement la constitution (Figure 7).
Figure 7. Théodolite ZEISS T1

 Le
tachéomètre combine un théodolite et un dispositif de mesure de distance.
Celui-ci peut être intégré à la lunette, ou indépendant et fixé au dessus de la
lunette. Dans ce second cas, les systèmes de visée et de mesure de distance
sont placés sur des axes parallèles : il est alors nécessaire de prendre
en compte le déport entre les deux, extrêmement important sur les visées
courtes. Les principes de la tachéométrie électronique sont relativement
simples, et nous nous y limiterons (informations issues du Lexique
Topographique de l’AFT).
Le
tachéomètre combine un théodolite et un dispositif de mesure de distance.
Celui-ci peut être intégré à la lunette, ou indépendant et fixé au dessus de la
lunette. Dans ce second cas, les systèmes de visée et de mesure de distance
sont placés sur des axes parallèles : il est alors nécessaire de prendre
en compte le déport entre les deux, extrêmement important sur les visées
courtes. Les principes de la tachéométrie électronique sont relativement
simples, et nous nous y limiterons (informations issues du Lexique
Topographique de l’AFT).
Le dispositif de mesure électronique des longueurs est appelé distancemètre. L’émetteur produit un train d'ondes électromagnétiques et le récepteur analyse l’écho renvoyé par un réflecteur. L’onde émise est appelée onde porteuse, et fait l’objet d’une modulation. Le procédé de mesure consiste à comparer la phase de modulation de l’onde reçue à celle de l’onde émise après le trajet aller-retour.
Plus concrètement, la mesure est réalisée par une émission successive de plusieurs fréquences distinctes, permettant ainsi de lever l’ambiguïté sur le nombre de cycles entre l’émetteur et le réflecteur. Les réflecteurs les plus souvent utilisés sont des coins de cubes, ou prismes rhomboédriques.
Un complément sur la tachéométrie est fourni
dans un document tiré à part.
3.3.4. Les réseaux de référence
Le réseau RGF est structuré hiérarchiquement en 3 parties : les réseaux de référence, de base et de détails.
Le RRF : Réseau de Référence Français
· 23 points déterminés par géodésie spatiale de grande précision (précision 10-7).
· observations entre 1989 et 1993
· mai 1989 : observations GPS pour le réseau européen (93 points en Europe, 8 en France)
· juin 1989 : observations VLBI pour le réseau européen (6 points dont 2 en France)
· 1992 : observations VLBI (1 point en France)
· 1993 : observations GPS des 23 points du RRF
Le RBF : Réseau de Base Français
· 1 009 sites déterminés par technique GPS (précision 10-6)
· observations en 1994, 1995 et 1996
Le RDF : Réseau de Détail Français (en cours de réalisation)
· constitué en particulier de points de la NTF et de canevas géodésiques appuyés sur le RBF
Figure 8. Le réseau RGF 93
 Depuis
décembre 2000, le système en vigueur en France est le RGF 93. Il dispose
d’un jeu de paramètres donnant au système cartographique français une meilleure
compatibilité avec le système GPS et le système WGS 84 qui lui est associé.
Datum géodésique global, il est doté d’une projection plane : la
projection Lambert 93. Elle est valable pour l’ensemble du territoire national.
Tous les paramètres sont rappelés dans le tableau suivant (Tableau 1). D’autre part, pour l’altimétrie, le RGF 93 est doté
d’un modèle de géoïde : le QGF98 (Quasi Géoïde Français).
Depuis
décembre 2000, le système en vigueur en France est le RGF 93. Il dispose
d’un jeu de paramètres donnant au système cartographique français une meilleure
compatibilité avec le système GPS et le système WGS 84 qui lui est associé.
Datum géodésique global, il est doté d’une projection plane : la
projection Lambert 93. Elle est valable pour l’ensemble du territoire national.
Tous les paramètres sont rappelés dans le tableau suivant (Tableau 1). D’autre part, pour l’altimétrie, le RGF 93 est doté
d’un modèle de géoïde : le QGF98 (Quasi Géoïde Français).
Ce système succède à la NTF (Nouvelle Triangulation de la France) qui avait consacré dans les administrations et chez les professionnels l’emploi de la projection Lambert par zone (Tableau 1), et plus récemment, le Lambert II Etendu, applicable sur l’ensemble du territoire. Cependant, même si l’obligation légale pour les travaux topographiques est d’employer le RGF 93, la loi prévoit une certaine souplesse. La fourniture de données dans tout système géodésique est envisageable, dès lors que les formules de transformation vers le RGF 93 sont fournies.
|
Zone Lambert |
I |
II |
III |
IV |
II étendu |
|
Zone application |
53.5gr - 57gr |
50.5gr - 53.5gr |
47gr - 50.5gr |
Corse |
France entière |
|
Latitude origine |
55gr = 49°30´ |
52gr = 46°48´ |
49gr = 44°06´ |
46.85gr = 42°09´54" |
52gr = 46°48´ |
|
Longitude origine |
0gr Paris |
0gr Paris |
0gr Paris |
0gr Paris |
0gr Paris |
|
Parallèles |
48°35´54.682" |
45°53´56.108" |
43°11´57.449" |
41°33´37.396" |
45°53´56.108" |
|
X0 : False
Easting |
600 000 m |
600 000 m |
600 000 m |
234.358 m |
600 000 m |
|
Y0 : False
Northing |
200 000 m |
200 000 m |
200 000 m |
185 861.369 m |
2 200 000 m |
Tableau 1. Les paramètres des projections françaises (IGN)
3.3.5. Les sources d’information
En France, la meilleure source d’information sur les référentiels reste l’Institut Géographique National, et les sites qui en dépendent. Sur son site Internet, on peut notamment accéder gratuitement :
· aux coordonnées des communes de France, ainsi qu’à toute une série d’informations collatérales :
· les numéros de cartes couvrant la commune (du 1/25.000 au 1/100.000)
· un accès vers la liste des missions de couverture photographique aérienne
· aux fiches signalétiques de points (planimétrie et altimétrie), à partir du numéro de la coupure 1/50.000 couvrant la zone
· la totalité des paramètres géodésiques actuellement et historiquement en vigueur en France, les moyens de transformation (formules, logiciel CIRCE 2000 de calculs de coordonnées RGF 93)
· une série de définitions et d’aide sémantique sur les termes et notions de géodésie.
TD : calcul d’un
cheminement polygonal
3.4. Détermination de l’incertitude de mesure
Une mesure est entachée d’une certaine erreur, d’une incertitude. Elle provient de divers facteurs : la méthode utilisée, l’instrument employé, l’expérience de l’opérateur, la grandeur mesurée… Différentes notions sont utilisées pour qualifier la qualité de la mesure, et divers moyens existent pour répartir les résidus d’une série de mesure.
Nous avons jusqu’ici parlé de fautes, d’erreurs accidentelles et systématiques sans en donner une définition précise. Tous ces termes, bien que faisant partie du même champ sémantique, couvrent des notions différentes.
· La faute : manquement à une norme, aux règles d’une science, d’une technique (Petit Larousse). On parle de faute généralement à propos de l’opérateur, et peut être due à un manque de soin, le non respect des règles de base, le manque d’expérience…
· L’erreur systématique : se répète et se cumule à chaque mesure. Elle est le plus souvent due aux imprécisions de l’instrument (qualité des composants, défauts de réglages…) et aux contraintes de sa mise œuvre. L’influence de ces erreurs peut souvent être évaluée par calcul, et prise en compte dans la détermination finale.
· L’erreur accidentelle : de valeur et de signe aléatoires, elle peut avoir diverses origines : défaut de calage de l’appareil à la mise en station, erreur de pointé, de lecture, des paramètres extérieurs non maîtrisables (température, hygrométrie…), erreur de réfraction accidentelle…
Sur une série de mesures (cheminement altimétrique, polygonal), l’influence des erreurs systématiques doit être minimisée par la méthode employée. Par contre, il reste les erreurs accidentelles qui sont généralement considérées comme les seules participant aux fermetures.
3.4.2. Méthodes de compensation
Tout protocole de mesure génère des erreurs. Il est capital d’identifier, quantifier et réduire les erreurs systématiques, mais les erreurs accidentelles doivent être réparties sur l’ensemble. Plusieurs méthodes sont possibles, mais partent toutes globalement de l’hypothèse de l’équiprobabilité de chaque source d’erreur accidentelle lors de chaque mesure. Par exemple, sur un cheminement altimétrique, la probabilité de faire une erreur de lecture sur mire est identique qu’il s’agisse de la première ou de la nième dénivelée.
3.4.2.1. Compensation proportionnelle
C’est le mode de compensation le plus simple. Il exploite l’hypothèse d’équiprobabilité au mot : l’erreur globale constatée sur la série de mesures est la résultante des erreurs sur chaque mesure de la série. Par conséquent, la fermeture est répartie sur chaque mesure individuelle. Pour une fermeture f obtenue sur n mesures, la correction à appliquer aux observations est alors donnée par :
![]() [Eq.
13]
[Eq.
13]
Elle peut s’avérer tout à fait suffisante pour la répartition de la fermeture d’un nivellement géométrique à portées strictement équidistantes et équivalentes.
3.4.2.2. Compensation pondérée
La compensation pondérée est une amélioration de la compensation proportionnelle. Elle prend en compte, par la pondération des observations, une certaine appréciation de la qualité des mesures. Tout le problème est alors de déterminer le facteur significatif agissant sur cette qualité. De même que précédemment, la correction à appliquer à la jième observation sur n, de facteur de pondération p, est donnée par :
 [Eq.
14]
[Eq.
14]
Dans le cas d’un tour d’horizon, on pourra prendre la distance au point comme facteur de pondération. En effet, en triangulation, le pointé sur des cibles lointaines est souvent bien plus précis que sur des cibles proches.
3.4.2.3. Compensation par les moindres carrés
Les méthodes précédentes s’appliquent dans les cas simples, où les mesures redondantes ne sont que peu ou pas présentes. Dès lors que l’on s’intéresse à un réseau de mesures, engendrant des déterminations multiples d’une même grandeur, il est impératif de pouvoir tirer parti de l’ensemble des observations sans créer de discordances entre elles.
Le principe des moindres carrés a pour objectif de minimiser les carrés des écarts entre les observations et la valeur vraie de la grandeur observée. Elle se base exclusivement sur la redondance de mesures. Un calcul abouti par moindres carrés donne accès à la valeur la plus probable de la grandeur mesurée, avec un indicateur de qualité primordial : l’erreur moyenne quadratique (souvent notée emq ; en anglais, rmse, root mean square error).
La complexité de la méthode ne nous permet pas de la présenter dans le détail. Nous nous limiterons par conséquent à une expression simplifiée, matricielle. La première étape est de définir des valeurs approchées des inconnues, pour pouvoir écrire la matrice V des écarts avec chaque mesure. Ensuite, l’équation suivante donne les appoints à apporter aux valeurs approchées pour obtenir les valeurs les plus probables, compte tenu des observations réalisées.
![]() [Eq.
15]
[Eq.
15]
Ainsi, l’erreur moyenne quadratique du calcul (mq0), également dite réduite à l’unité de poids, est donné par la relation :
 [Eq.
16]
[Eq.
16]
avec p le poids de l’observation, v l’écart entre valeurs approchée et observée, n le nombre total d’observations, q le nombre d’observations strictement nécessaires au calcul de l’inconnue.
TD : compensation d’un nivellement et d’une polygonale


